[MIGRATE] MCMC

蒙特卡洛方法（Monte Carlo）是一种通过特定分布下的随机数（或伪随机数）进行模拟的方法。典型的例子有蒲丰投针、定积分计算等等，其基础是大数定律。

蒙特卡洛方法有哪些优缺点如下：

• 优点：计算准确性由采样的均匀程度决定；大大简化问题复杂性
• 缺点：
  • 由于要进行大量的抽样计算，对计算机速度依赖性强
  • 目前绝大多数随机数发生器均为伪随机数，一定程度上有偏
  • 定积分求解问题中，对于$\color{blue}{复杂或者高维的分布}$，利用蒙特卡洛方法生成随机样本非常困难

　　蒙特卡罗方法在金融工程学，宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算、核工程)等领域应用广泛。

在蒙特卡洛模拟中，我们在后验分布中抽取样本，当这些样本独立时，利用大数定律样本均值会收敛到期望值。如果得到的样本是不独立的，那么就要借助于马尔科夫链进行抽样。马尔科夫链又称为马尔科夫过程是一种离散的随机过程，随机过程可以看做一个随时间变化的随机变量序列。

对一个马尔科夫链来说，未来状态只与当前t时刻有关，而与t时刻之前的历史状态无关。马尔科夫链的每个状态的状态转移概率构成了其状态转移矩阵\(P\)

当步长$n$足够大时，一个非周期且任意状态联通的马氏链可以收敛到一个平稳分布\(\pi(x)\) ，马氏链收敛定理是MCMC的基础。

MCMC方法就是构造合适的马尔科夫链进行抽样而使用蒙特卡洛方法进行积分计算。 既然马尔科夫链可以收敛到平稳分布。我们可以建立一个以$π$为平稳分布的马尔科夫链，对这个链运行足够长时间之后，可以达到平稳状态。此时马尔科夫链的值就相当于在分布$π(x)$中抽取样本。利用马尔科夫链进行随机模拟的方法就是MCMC。

MCMC的主要问题是：如何构造转移矩阵\(P\),使得平稳分布恰好是我们要的分布$π (x)$。由此，我们首先有了M-H算法，它用到可马尔科夫链的另一个性质，如果具有转移矩阵$P$和分布$π(x)$的马氏链对所有的状态$i,j$满足下面的等式：

这个等式称为细致平衡方程，此时该马氏链的分布$π(x)$是平稳的。一般情况下，任意给的$π(x)$不一定平稳，那么可以构造函数\(\alpha(i,j)\),使得：

此时取$α(i,j) = π(j)P(j,i)$，$α(j,i) = π(i)P(i,j)$时等式(2)必然成立。

(2)式中的$α(i,j)$又叫接受率，是接受状态从$i$转移到$j$的概率。如果$α$过小，将会导致频繁拒绝转移，马氏链难以收敛，所以我们考虑放大$α$，使得$α(i,j)$和$α(j,i)$中大的值为$1$，小的值同比放大为$\frac{\pi(j)P(j,i)}{\pi(i)P(i,j)}$，那么$α(i,j) = min\{1,\frac{\pi(j)P(j,i)}{\pi(i)P(i,j)}\}$。在马尔科夫链状态转移过程中，我们以概率$α(i,j)$接受转移，从而得到最终的稳定分布，这种算法称为M-H算法。

M-H算法需要提前构造提议分布(proposal distribution)$π(x)$，然后经过提议分布采样后计算出接受概率，对采样进行接受或是拒绝，最后得到服从特定分布的样本。优点是通过构造精妙的马尔科夫链，提高了抽样的效率，尤其是面对条件分布抽样时。缺点是需要找到合适的提议分布，而且收敛速度可能较慢。

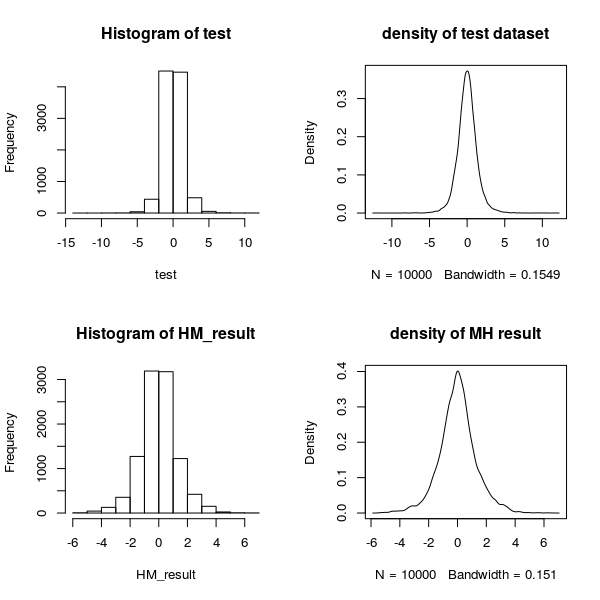
现欲对自由度为5的t分布抽取10000个样本，我们分别用M-H算法和R语言自带的t分布抽样命令rt进行抽样，然后对比二者结果。

对于M-H抽样，我们选择标准正态分布为其提议分布，进行10000次模拟，R语言代码和得到结果如下：

ptm <- proc.time()
#### M-H algorithm ####
N = 10000  
x = vector(length = N)  
x[1] = 0  
# uniform variable: u  
u = runif(N)  
sd = 1
df = 5  
# sample the student distrubution with 5 freedom
for (i in 2:N)  {  
  y = rnorm(1,mean = x[i-1],sd = sd)
  p_accept = dt(y,df) * pnorm(x[i-1],y,sd) / pnorm(x[i-1],y,sd) / (dt(x[i-1],df))
  if ((u[i] <= p_accept))  
  {  x[i] = y  }  
  else  
  { x[i] = x[i-1] }  
}  
HM_result <- x
proc.time()-ptm

#plot(x,type = 'l')  
test = rt(10000,5)
par(mfrow=c(2,2)) 
hist(test)
plot(density(test),main = "density of test dataset")
hist(HM_result)
plot(density(HM_result),main = "density of MH result")

M-H抽样在较低维度值运算中是比较方便的，然而在维数较高时，选择适当的提议分布并非易事，而Gibbs抽样仅仅需要了解满条件分布(full conditi- onal　distribution)，因此在高维积分时更具有优势（朱慧明 等, 《贝叶斯计量经济模型》, 2009,科学出版社）。

n维变量的Gibbs抽样方法如下:给定抽样初始点\(x^{(0)} = (x_1^{(0)},x_2^{(0)},...,x_n^{(0)}\) $)$，并假设第$t-1$次迭代的迭代值为$x^{(t-1)}$，则第$t$次迭代由以下步骤完成：

• 由满条件分布$π(x_1 | x_2^{(t-1)},…,x_n^{(t-1)})$抽取\(x_1^{(t)}\)
• 由满条件分布$π(x_2 | x_1^{(t-1)},x_3^{(t-1)}…,x_n^{(t-1)})$抽取\(x_2^{(t)}\)
• … …
• 由满条件分布$π(x_n | x_1^{(t-1)},…,x_{n-1}^{(t-1)})$抽取\(x_n^{(t)}\)

　　至此完成$t-1$到$t$的一次迭代，重复迭代直到$x^{(t)}$分布稳定后即可。

以二维正态分布抽样为例，不妨设$X = (X_1,X_2)$服从二元正态分布，即:

则有:

• $x_2^{(t+1)}| x_1^{(t+1)} ∼ N(ρ x_1^{t+1},1-ρ^2) $
• \(x_1^{(t+1)} | x_2^{(t+1)} \sim N(\rho x_2^{t+1},1-\rho^2)\)

　　并且可以证明：

　　当$t → ∞\(时，\)(x_1^{t},x_2^{t})$的分布将收敛到目标分布。R语言代码和结果如下：

n <- 5000 #抽样个数
n_1 <- 2500 # 收敛个数
X <- matrix(0, n, 2)
mu1 <- 0 
mu2 <- 0
sigma1 <- 1
sigma2 <- 1
rho <- 0.5
s1.c <- sqrt(1 - rho^2) * sigma1
s2.c <- sqrt(1 - rho^2) * sigma2
X[1, ] <- c(mu1, mu2) #初始化
for (i in 2:n) {
  x2 <- X[i - 1, 2]
  m1.c <- mu1 + rho * (x2 - mu2) * sigma1/sigma2
  X[i, 1] <- rnorm(1, m1.c, s1.c)
  x1 <- X[i, 1]
  m2.c <- mu2 + rho * (x1 - mu1) * sigma2/sigma1
  X[i, 2] <- rnorm(1, m2.c, s2.c)
}
b <- n_1 + 1
x.mcmc <- X[b:n, ]
library(MASS)
MVN.kdensity <- kde2d(x.mcmc[, 1], x.mcmc[, 2], h = 5) #估计核密度
par(mfrow=c(2,2)) 
plot(x.mcmc, col = "blue", xlab = "X1", ylab = "X2") #绘制二元正态分布等高线图
contour(MVN.kdensity, add = TRUE)
hist(x.mcmc[, 1],main = "histogram of x1")
hist(x.mcmc[, 2],mian = "histogram of x2")
x<-y<-seq(-4,4,length=20)
f<-function(x,y){(exp(-0.5*x^2-0.5*y^2))/(2*pi)}
z<-outer(x,y,f)
persp(x,y,z,theta=45,phi=25,col='lightblue')