[MIGRATE] PCA主成分分析

　　对于样本 \(i \in N\) 有 \(p\) 维特征 \(X_{p \times 1}\) ，于是有$p$维主成分 \(Z_{p \times 1}\) ，以及参数 \(\theta_{p \times p}\) 满足：

　　其中 \(Z_1 = Z[0]\) 便是样本 \(i\) 的第一主成分值，以此类推。 \(\theta\) 可以看做是对原坐标系的正交变换，参数估计方法后面会详细讨论。针对上述三点的性质，分别对应有：

• \(Cov(Z_i,Z_j)=0~~~i,j = 1,2, \cdots,p~and~i \neq j\)
• \(\sum_{i =1}^{p}{\theta_{ij}^2} = 1~~~j = 1,2,\cdots,p\)
• \(Var(Z_i) = max(Var(\theta_i X))\) and \(Var(Z_i)>Var(Z_j)\) if \(i \lt j\)

　　问题转换为，如何在满足以上性质下找到合适的 \(\theta\)

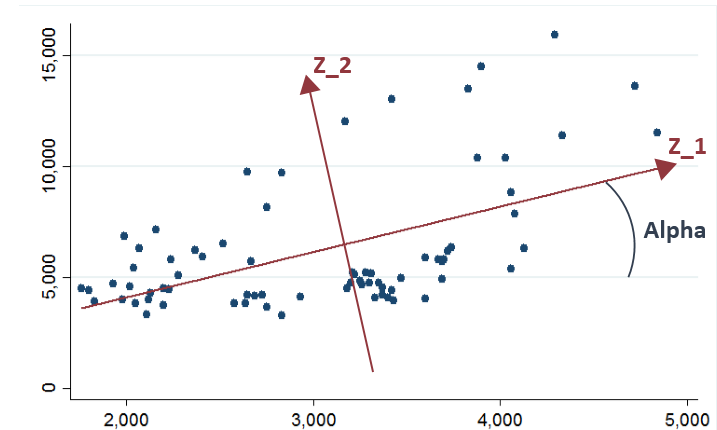
　　将原本二维空间以角 \(\alpha\) 旋转得到新坐标轴，此时在两轴上投影即主成分，我们可以写出此时 \(X\) 与 \(Z\) 的关系：

　　参数$θ$可以写成如下矩阵：

　　从上图可以看出，二维平面上点的波动大部分可以归结为$Z_1$的波动，小部分可以归结为$Z_2$的波动，这样一来，二维问题可以降维至一维，只看$Z_1$，因为其反应了大部分信息。

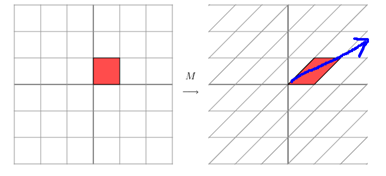
　　对于上述示例的向量$X=\begin{bmatrix} X_1 \\ X_2 \end{bmatrix}$，用参数矩阵$θ$左乘\(X\),即是对向量所在轴进行拉伸变换，而其对角线方向即变换的主要方向，这个方向就是变换后的$Z_1$轴，见下图，因此“如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了”。

　　如果说一个向量$v$是方阵$A$的特征向量，那么一定有：

　　从这个公式可以看出，特征值所对应的特征向量描绘了此变换的方向，而特征值描绘了此变换的大小，或者说此变换方向对整体方向的贡献值。特征分解满足：

　　其中A为方阵，Q为特征向量矩阵，每一列均为一个特征向量，$Σ$为特征值为对角元素的对角阵，与特征向量一一对应。特征值求法如下：

　　其中 \(\lambda\) 为特征值，带入下式后得到特征值对应的特征向量 \(v\),\(E\) 为单位阵。

　　由主成分性质，求第一主成分 \(Z_1 = \theta_1 X\) 的问题，即为求$θ_1$使得在 \(\theta_1 \theta_1'=1\) 下 \(Var(Z_1)\) 达到最大，其中 \(\theta_1\) 表示参数矩阵 \(\theta\) 的第一行，这是条件极值问题，用拉格朗日乘子法求解下式极值：

　　\(\Sigma\) 为随机向量$X$的协方差矩阵，对 \(\theta_1\) 求偏导后得到 \(2(\Sigma - \lambda E)\theta_1 = 0\) ,由于 \(\theta_1 \neq 0\) ,所以转换为求 \(|\Sigma-\lambda E |=0\) ，即求 \(\Sigma\) 特征值和特征矩阵的问题。

　　设随机向量 \(X=(X_1,X_2,X_3)'\) 的协方差矩阵 \(\Sigma\) 如下，对 \(X\) 进行主成分分析：

　　求得 \(\Sigma\) 的特征值从大到小依次为 \(\lambda_1 = 3+\sqrt{8},\lambda_2 = 2,\lambda_3 = 3-\sqrt{8}\) ，相对应的单位正交( $θ θ' = E $ )特征向量为：

　　因此，主成分为：

　　\(Z_1\) 对X的贡献率可达 \(\frac{3+\sqrt{8}}{3+\sqrt{8}+2+3-\sqrt{8}} = 72.8\%\) ，而$Z_2$的贡献率为25\%， \(Z_1,Z_2\) 的联合贡献率为 97.85\%，我们可以认为这两个变量以及反映了原变量绝大多数信息，从而实现从三维降到二维的过程。 　　

　　在现实生活中，由于样本的高维特征（图像识别每一个像素点都是一个维度），将会导致协方差矩阵$Σ$非常大，计算机难以存储与计算，那如何针对高维数据做特征值分解呢，我们知道 \(\Sigma = X X'\) ，考虑替代矩阵 \(P = X' X\) ，如果有100个样本，10000个维度，那么 \(\Sigma\) 就是一个10000维方阵，而$P$只是一个100维方阵。我们做如下推导：

　　这样通过求$P$的特征值和特征向量，其特征值即 \(\Sigma\) 的特征值，其特征向量右乘随机向量 \(X\) 即为 \(\Sigma\) 的特征向量，从而完成高维数据的特征值分解（只能得到部分前几的主成分）。

　　计算机在求解方阵的特征值分解时，利用QR分解进行迭代，具体步骤如下^{1, 2}：

1. 将实对称矩阵利用Householder变换法化为三对角矩阵
2. 用吉文斯变换实现一次等效的QR迭代
3. 增加迭代次数直至收敛

Python有着非常强大的科学计算库：

• numpy~~基础计算库，多维数组处理
• scipy~~基于numpy，用于数值计算等等，默认调用intel mkl（高度优化的数学库）
• pandas~~强大的数据框，基于numpy
• matplotlib~~绘图库,基于numpy,scipy
• sklearn~~机器学习库，有各种机器学习算法

　　如果你仅仅装了numpy，那么计算特征值效率极低，5000维要41秒，10000维溢出。但是如果装了numpy+mkl,那么5000维将缩短至0.28秒，10000维1.5秒。mkl包含了blas,~lapack这些效率极高的线性代数库，你也可以尝试配置ATLAS环境（matlab的矩阵运算环境）。 　　另外，有一些好用的高度集成的科学计算IDE ：Anaconda, ~Canopy

　　下面利用PCA提取如下三幅300*400像素的图片的主成分，由于每张图片有120000个维度，难以进行特征值分解，所以采用上述高维数据的特征分解法：

python代码如下：

# -*- coding: utf-8 -*-
import numpy as np
import scipy.linalg as linA # 为了激活线性代数库mkl
from PIL import Image
import os,glob

def sim_distance(train,test):
    '''
    计算欧氏距离相似度
    :param train: 二维训练集
    :param test: 一维测试集
    :return: 该测试集到每一个训练集的欧氏距离
    '''
    return [np.linalg.norm(i - test) for i in train]

picture_path = os.getcwd()+'\\pictures\\'
array_list = []
for name in glob.glob(picture_path+'*.jpg'):
    # 读取每张图片并生成灰度（0-255）的一维序列 1*120000
    img = Image.open(name)
    # img_binary = img.convert('1') 二值化
    img_grey = img.convert('L') # 灰度化
    array_list.append(np.array(img_grey).reshape((1,120000)))

mat = np.vstack((array_list)) # 将上述多个一维序列合并成矩阵 3*120000
P = np.dot(mat,mat.transpose()) # 计算P
v,d = np.linalg.eig(P) # 计算P的特征值和特征向量
d= np.dot(mat.transpose(),d) # 计算Sigma的特征向量 12000 * 3
train = np.dot(d.transpose(),mat.transpose()) # 计算训练集的主成分值 3*3

# 开始测试
test_pic = np.array(Image.open('c.jpg').convert('L')).reshape((1,120000))
result = sim_distance(train.transpose(),np.dot(test_pic,d))
print result
test_pic = np.array(Image.open('e.jpg').convert('L')).reshape((1,120000))
result = sim_distance(train.transpose(),np.dot(test_pic,d))
print result

　　计算得到前三特征值为：

　　对应的特征矩阵 \(\theta_{120000 \times 3}\) 为：

　　通过 \(\theta'X\) 得到三张图片在三个主轴上的值分别为：

　　利用如下图片进行识别测试，首先右乘 \(\theta'\) 得到各自在三个主轴上的值，然后计算出该图片到训练样本中的三张图片的欧式距离：

　　显然，根据计算结果，我们认为左图更像人一点~~O(∩_∩)O，一个简单的利用PCA进行图像识别的小程序就此完成，当然这个非常粗糙，但对于理解PCA有着较大的帮助。